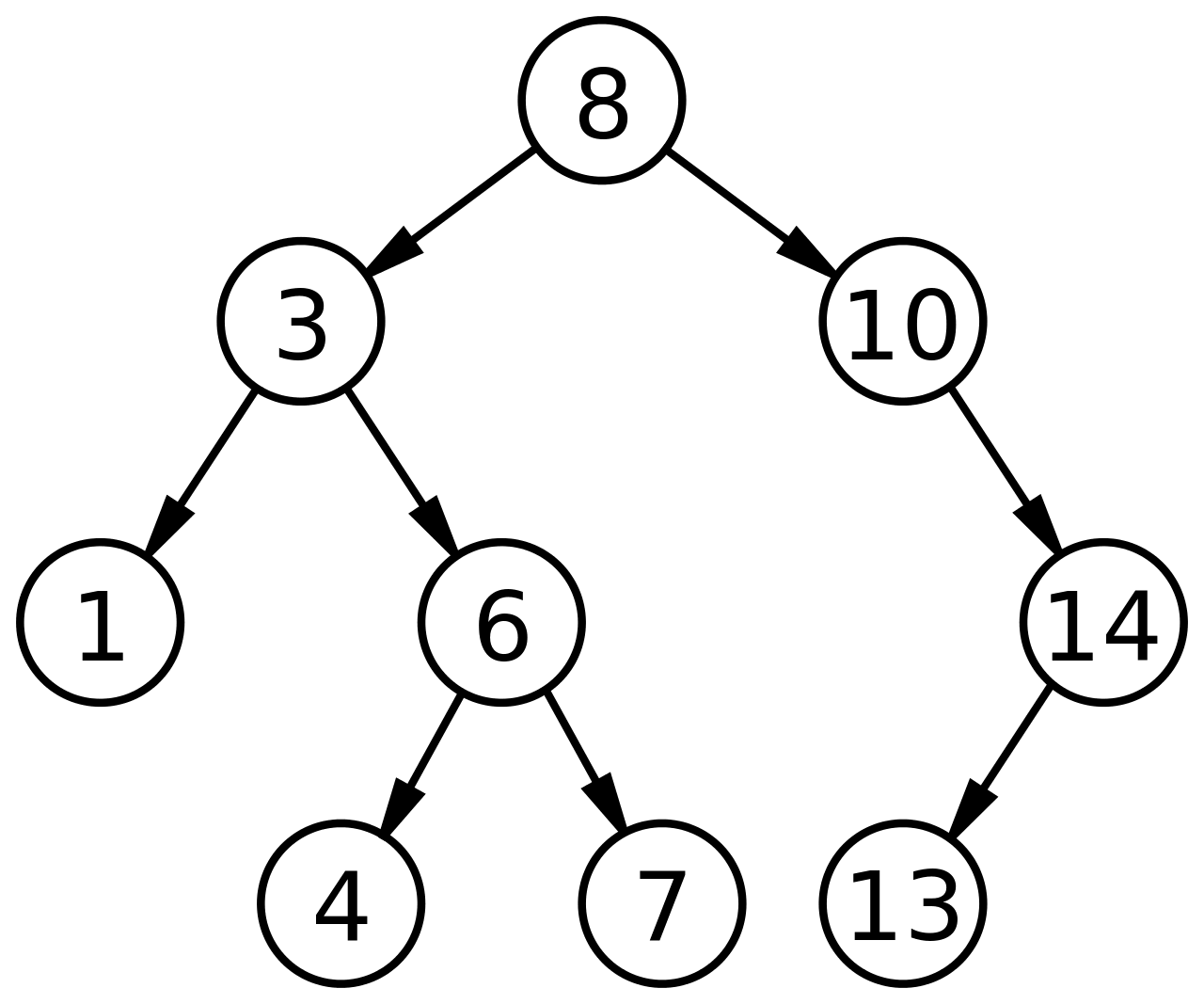
二叉搜索树及其遍历

排序类型

前序遍历（根节点 > 左子树 > 右子树）：8 => 3 => 1 => 6 => 4 => 7 => 10 => 14 => 13
中序遍历（左子树 > 根节点 > 右子树）：1 => 3 => 4 => 6 => 7 => 8 => 10 => 13 => 14
后序遍历（左子树 > 右子树 > 根节点）：1 => 4 => 7 => 6 => 3 => 13 => 14 => 10 => 8
层次遍历（从上往下一层层来）：8 => 3 => 10 => 1 => 6 => 14 => 4 => 7 => 13

二叉树的构造

javascript

// 节点对象的构造函数
function Node(data, left, right) {
  this.data = data;
  this.left = left;
  this.right = right;
}

Node.prototype.getData = function () {
  return this.data;
};

// 二叉搜索树的构造函数
function BST() {
  this.root = null;
}

// 插入方法
BST.prototype.insert = function (data) {
  const n = new Node(data, null, null);
  if (this.root === null) {
    this.root = n;
    return;
  }
  let current = this.root;
  let parent;
  while (true) {
    parent = current;
    if (data < current.data) {
      current = current.left;
      if (current === null) {
        parent.left = n;
        break;
      }
    } else {
      current = current.right;
      if (current === null) {
        parent.right = n;
        break;
      }
    }
  }
};

const nums = new BST();
nums.insert(8);
nums.insert(3);
nums.insert(10);
nums.insert(1);
nums.insert(6);
nums.insert(14);
nums.insert(4);
nums.insert(7);
nums.insert(13);

前/中/后序遍历的递归实现

这个算法很好实现：

javascript

// 前序遍历二叉树
BST.prototype.preOrder = function (node) {
  if (node !== null) {
    console.log(node.getData());
    this.preOrder(node.left);
    this.preOrder(node.right);
  }
};

// 中序遍历二叉树
BST.prototype.inOrder = function (node) {
  if (node !== null) {
    this.inOrder(node.left);
    console.log(node.getData());
    this.inOrder(node.right);
  }
};

// 后序遍历二叉树
BST.prototype.postOrder = function (node) {
  if (node !== null) {
    this.postOrder(node.left);
    this.postOrder(node.right);
    console.log(node.getData());
  }
};

// 测试

nums.inOrder(nums.root);

// 依次输出如下内容：
// 1 3 4 6 7 8 10 13 14

前序遍历的非递归实现

根据前序遍历访问的顺序，优先访问根结点，然后再分别访问左孩子和右孩子。即对于任一结点，其可看做是根结点，因此可以直接访问，访问完之后，若其左孩子不为空，按相同规则访问它的左子树；访问其左子树后，再访问它的右子树。因此其处理过程如下：

对于任一结点P：

访问结点P，并将结点P入栈;
判断结点P的左孩子是否为空，

若为空，则取栈顶结点并进行出栈操作，并将栈顶结点的右孩子置为当前的结点P，循环至1；
若不为空，则将P的左孩子置为当前的结点P;

直到P为NULL并且栈为空，则遍历结束。

javascript

function preOrder(bst) {
  let p = bst.root;
  const arr = [];
  while (p !== null || arr.length > 0) {
    while (p !== null) {
      console.log(p.getData());
      arr.push(p);
      p = p.left;
    }

    if (arr.length > 0) {
      p = arr.pop();
      p = p.right;
    }
  }
}

中序遍历的非递归实现

根据中序遍历的顺序，对于任一结点，优先访问其左孩子，而左孩子结点又可以看做一根结点，然后继续访问其左孩子结点，直到遇到左孩子结点为空的结点才进行访问，然后按相同的规则访问其右子树。因此其处理过程如下：

对于任一结点P，

若其左孩子不为空，则将P入栈并将P的左孩子置为当前的P，然后对当前结点P再进行相同的处理；
若其左孩子为空，则取栈顶元素并进行出栈操作，访问该栈顶结点，然后将当前的P置为栈顶结点的右孩子；
直到P为NULL并且栈为空则遍历结束。

javascript

function inOrder(bst) {
  let p = bst.root;
  const arr = [];
  while (p !== null || arr.length > 0) {
    while (p !== null) {
      arr.push(p);
      p = p.left;
    }

    if (arr.length > 0) {
      p = arr.pop();
      console.log(p.getData());
      p = p.right;
    }
  }
}

后序遍历的非递归实现

后续遍历比前中/序遍历是要麻烦一些的。

遍历顺序：左右根。左路的遍历和上面的思路是类似的，区别是元素出栈时不能直接打印，因为如果有没访问过右侧子树的话，需要先访问右侧子树。右侧子树访问结束后才访问根节点。

javascript

function postOrder(bst) {
  let p = bst.root;
  let last = null;
  const arr = [];
  while (p !== null || arr.length > 0) {
    while (p !== null) {
      arr.push(p);
      p = p.left;
    }

    if (arr.length > 0) {
      p = arr[arr.length - 1]; // 栈顶元素
      // 当p不存在右子树或右子树已被访问过的话，直接访问当前节点数据
      if (!p.right || p.right === last) {
        p = arr.pop();
        console.log(p.getData());
        last = p; // 记录上一次访问过的节点
        p = null; // 这个容易漏掉，避免下个循环继续访问左子树
      } else {
        p = p.right;
      }
    }
  }
}

层次遍历

递归方案

javascript

// 遍历到某个节点后，将该节点的值推入到指定深度对应的数组中
function level(node, idx, arr) {
  if (arr.length < idx) {
    arr.push([]);
  }

  arr[idx - 1].push(node.value);

  if (node.left !== null) {
    level(node.left, idx + 1, arr);
  }

  if (node.right !== null) {
    level(node.right, idx + 1, arr);
  }
}

function levelOrder(root) {
  if (root === null) {
    return [];
  }

  const arr = [];
  level(root, 1, arr);
  return arr;
}

非递归方案

使用队列实现。

javascript

function levelOrder(root) {
  const arr = [];
  if (root === null) {
    return arr;
  }

  const queue = [root];

  while (queue.length > 0) {
    const currentLevel = [];
    const currentLevelLength = queue.length;
    for (let i = 0; i <= currentLevelLength; i++) {
      const node = queue.pop();
      currentLevel.push(node.value);

      if (node.left !== null) {
        queue.push(node.left);
      }
      if (node.right !== null) {
        queue.push(node.right);
      }
    }
    arr.push(currentLevel);
  }

  return arr;
}

二叉搜索树及其遍历 ​

排序类型 ​

二叉树的构造 ​

前/中/后序遍历的递归实现 ​

前序遍历的非递归实现 ​

中序遍历的非递归实现 ​

后序遍历的非递归实现 ​

层次遍历 ​

二叉搜索树及其遍历

排序类型

二叉树的构造

前/中/后序遍历的递归实现

前序遍历的非递归实现

中序遍历的非递归实现

后序遍历的非递归实现

层次遍历